Defining Observing Constraints#
Contents#
Introduction to Built-In Constraints#
Frequently, we have a long list of targets that we want to observe, and we need
to know which ones are observable given a set of constraints imposed on our
observations by a wide range of limitations. For example, your telescope may
only point over a limited range of altitudes, your targets are only useful
in a range of airmasses, and they must be separated from the moon by some
large angle. The constraints module is here to help!
Say we’re planning to observe from Subaru Observatory in Hawaii on August 1,
2015 from 06:00-12:00 UTC. First, let’s set up an Observer object:
from astroplan import Observer, FixedTarget
from astropy.time import Time
subaru = Observer.at_site("Subaru")
time_range = Time(["2015-08-01 06:00", "2015-08-01 12:00"])
We’re keeping a list of targets in a text file called targets.txt, which
looks like this:
# name ra_degrees dec_degrees
Polaris 37.95456067 89.26410897
Vega 279.234734787 38.783688956
Albireo 292.68033548 27.959680072
Algol 47.042218553 40.955646675
Rigel 78.634467067 -8.201638365
Regulus 152.092962438 11.967208776
We’ll read in this list of targets using astropy.table, and create a list
of FixedTarget objects out of them:
# Read in the table of targets
from astropy.table import Table
target_table = Table.read('targets.txt', format='ascii')
# Create astroplan.FixedTarget objects for each one in the table
from astropy.coordinates import SkyCoord
import astropy.units as u
targets = [FixedTarget(coord=SkyCoord(ra=ra*u.deg, dec=dec*u.deg), name=name)
for name, ra, dec in target_table]
We will build a bulleted list of our constraints first, then implement them in code below.
Our observations with Subaru can only occur between altitudes of ~10-80 degrees, which we can define using the
AltitudeConstraintclass.We place an upper limit on the airmass of each target during observations using the
AirmassConstraintclass.Since we’re optical observers, we only want to observe targets at night, so we’ll also call the
AtNightConstraintclass. We’re not terribly worried about sky brightness for these bright stars, so we’ll define “night” times as those between civil twilights by using the class methodtwilight_civil:
from astroplan import (AltitudeConstraint, AirmassConstraint,
AtNightConstraint)
constraints = [AltitudeConstraint(10*u.deg, 80*u.deg),
AirmassConstraint(5), AtNightConstraint.twilight_civil()]
This list of constraints can now be applied to our target list to determine:
whether the targets are observable given the constraints at any times in the time range, using
is_observable,whether the targets are observable given the constraints at all times in the time range, using
is_always_observableduring what months the targets are ever observable given the constraints, using
months_observable:from astroplan import is_observable, is_always_observable, months_observable # Are targets *ever* observable in the time range? ever_observable = is_observable(constraints, subaru, targets, time_range=time_range) # Are targets *always* observable in the time range? always_observable = is_always_observable(constraints, subaru, targets, time_range=time_range) # During what months are the targets ever observable? best_months = months_observable(constraints, subaru, targets, time_range)
The is_observable and is_always_observable functions
will return boolean arrays which tell you whether or not each target is
observable given your constraints. Let’s print these results in tabular form:
>>> from astropy.table import Table
>>> import numpy as np
>>> observability_table = Table()
>>> observability_table['targets'] = [target.name for target in targets]
>>> observability_table['ever_observable'] = ever_observable
>>> observability_table['always_observable'] = always_observable
>>> print(observability_table)
<Table length=6>
targets ever_observable always_observable
str7 bool bool
------- --------------- -----------------
Polaris True True
Vega True True
Albireo True False
Algol True False
Rigel False False
Regulus False False
Now we can see which targets are observable! You can also use the
observability_table method to do the same calculations and
store the results in a table, all in one step:
>>> from astroplan import observability_table
>>> table = observability_table(constraints, subaru, targets, time_range=time_range)
>>> print(table)
target name ever observable always observable fraction of time observable
----------- --------------- ----------------- ---------------------------
Polaris True True 1.0
Vega True True 1.0
Albireo True False 0.833333333333
Algol True False 0.166666666667
Rigel False False 0.0
Regulus False False 0.0
Let’s sanity-check these results using plot_sky to plot
the positions of the targets throughout the time range:
(Source code, png, hires.png, pdf, svg)
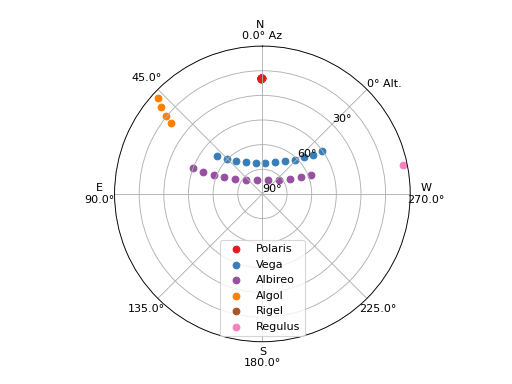
We can see that Vega is in the sweet spot in altitude and azimuth for this time range and is always observable. Albireo is not always observable given these criteria because it rises above 80 degrees altitude. Polaris hardly moves and is therefore always observable, and Algol starts out observable but sets below the lower altitude limit, and then the airmass limit. Rigel and Regulus never rise above those limits within the time range.
Visualizing Constraints#
Suppose an observer is planning to observe low-mass stars in Praesepe in the
optical and infrared from the W.M. Keck Observatory. The observing constraints
require all observations to occur (i) between astronomical twilights; (ii)
while the Moon is separated from Praesepe by at least 45 degrees; and (iii)
while Praesepe is above the lower elevation limit of Keck I, about 33 degrees.
These observing constraints can be specified with the
AtNightConstraint, MoonSeparationConstraint, and
AltitudeConstraint objects, like this:
We can evaluate the constraints at one hour intervals in a loop, to create an observability grid like so:
This kind of grid can be useful for visualizing what’s happening under-the-hood
when you use is_observable or is_always_observable.
Click the link below for the source code to produce the observability grid shown
below. Dark squares represent times when the observing constraint is not
satisfied.
(Source code, png, hires.png, pdf, svg)
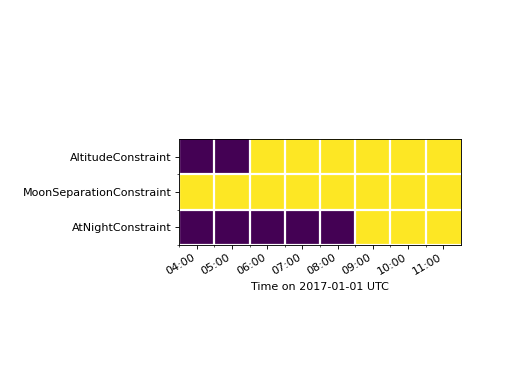
User-Defined Constraints#
There are many possible constraints that you could find useful which have
not been implemented (yet) in astroplan. This example will walk you through
creating your own constraint which will be compatible with the tools in the
constraints module.
We will begin by defining an observer at Subaru and reading the text file of stellar coordinates defined in the example above:
from astroplan import Observer, FixedTarget
from astropy.time import Time
subaru = Observer.at_site("Subaru")
time_range = Time(["2015-08-01 06:00", "2015-08-01 12:00"])
# Read in the table of targets
from astropy.io import ascii
target_table = ascii.read('targets.txt')
# Create astroplan.FixedTarget objects for each one in the table
from astropy.coordinates import SkyCoord
import astropy.units as u
targets = [FixedTarget(coord=SkyCoord(ra=ra*u.deg, dec=dec*u.deg), name=name)
for name, ra, dec in target_table]
In the previous section, you may have noticed that constraints are assembled by
making a list of calls to the initializers for classes like
AltitudeConstraint and AirmassConstraint. Each of
those constraint classes is subclassed from the abstract
Constraint class, and the custom constraint that we’re going to
write must be as well.
In this example, let’s design our constraint to ensure that all targets must
be within some angular separation from Vega – we’ll call it
VegaSeparationConstraint. Two methods, __init__ and
compute_constraint must be written for our constraint to work:
The
__init__method will accept the minimum and maximum acceptable separations a target could have from Vega.We’ll also define a method
compute_constraintswhich takes three arguments: aTimeor array of times to test, anObserverobject, and some targets (aSkyCoordobject representing a single target or a list of targets).compute_constraintswill return an array of booleans that describe whether or not each target meets the constraints. The super classConstrainthas a__call__method which will run your custom class’scompute_constraintsmethod when you check if a target is observable usingis_observableoris_always_observable. This__call__method also checks the arguments, converting singleFixedTargetor lists ofFixedTargetobjects into anSkyCoordobject. The__call__method ensures the returned array of booleans is the correct shape, socompute_constraintsshould not normally be called directly - use the__call__method instead.We also want to provide the option of having the constraint output a non-boolean score. Where being closer to the minimum separation returns a higher score than being closer to the maximum separation.
Here’s our VegaSeparationConstraint implementation:
from astroplan import Constraint, is_observable, min_best_rescale
from astropy.coordinates import Angle
import astropy.units as u
class VegaSeparationConstraint(Constraint):
"""
Constraint the separation from Vega
"""
def __init__(self, min=None, max=None, boolean_constraint=True):
"""
min : `~astropy.units.Quantity` or `None` (optional)
Minimum acceptable separation between Vega and target. `None`
indicates no limit.
max : `~astropy.units.Quantity` or `None` (optional)
Minimum acceptable separation between Vega and target. `None`
indicates no limit.
"""
self.min = min if min is not None else 0*u.deg
self.max = max if max is not None else 180*u.deg
self.boolean_constraint = boolean_constraint
def compute_constraint(self, times, observer, targets):
vega = SkyCoord(ra=279.23473479*u.deg, dec=38.78368896*u.deg)
# Calculate separation between target and vega
# Targets are automatically converted to SkyCoord objects
# by __call__ before compute_constraint is called.
vega_separation = vega.separation(targets)
if self.boolean_constraint:
mask = ((self.min < vega_separation) & (vega_separation < self.max))
return mask
# if we want to return a non-boolean score
else:
# rescale the vega_separation values so that they become
# scores between zero and one
rescale = min_best_rescale(vega_separation, self.min,
self.max, less_than_min=0)
return rescale
Then as in the earlier example, we can call our constraint:
>>> constraints = [VegaSeparationConstraint(min=5*u.deg, max=30*u.deg)]
>>> observability = is_observable(constraints, subaru, targets,
... time_range=time_range)
>>> print(observability)
[False False True False False False]
The resulting list of booleans indicates that the only target separated by 5 and 30 degrees from Vega is Albireo. Following this pattern, you can design arbitrarily complex criteria for constraints.
By default, calling a constraint will try to broadcast the time and target arrays
against each other, and raise a ValueError if this is not possible. To see the
(target x time) array for the constraint, there is an optional grid_times_targets
argument. Here we find the (target x time) array for the non-boolean score:
>>> constraint = VegaSeparationConstraint(min=5*u.deg, max=30*u.deg,
... boolean_constraint=False)
>>> print(constraint(subaru, targets, time_range=time_range,
... grid_times_targets=True))
[[ 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. ]
[ 0.57748686 0.57748686 0.57748686 0.57748686 0.57748686 0.57748686
0.57748686 0.57748686 0.57748686 0.57748686 0.57748686 0.57748686]
[ 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. ]]
The score of .5775 for Albireo indicates that it is slightly closer to the 5 degree minimum than to the 30 degree maximum.